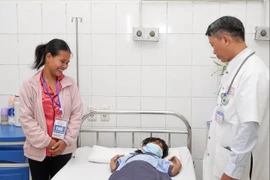
Một nhà toán học người Australia đã phát hiện ra ví dụ lâu đời nhất được biết đến về hình học ứng dụng, trên một viên đất sét Babylon 3.700 năm tuổi - và ông gọi đó là 'máy tính bảng' cổ đại.
Được biết đến với cái tên Si.427, chiếc máy tính bảng này mang một sơ đồ thực địa đo ranh giới của một số vùng đất.
Máy tính bảng Si.427 có niên đại từ thời Babylon Cổ giữa năm 1900 và 1600 trước Công nguyên và được phát hiện vào cuối thế kỷ 19 ở khu vực ngày nay là Baghdad, Iraq. Nó đã được đặt trong Bảo tàng Khảo cổ học Istanbul (Thổ Nhĩ Kỳ) trước khi Tiến sĩ Daniel Mansfield từ Đại học New South Wales (Australia) lần ra nó.

Tầm quan trọng của chiếc máy tính bảng này vẫn chưa được biết cho đến khi công trình của Tiến sĩ Mansfield được tiết lộ. Ảnh: UNSW Sydney
Trước đó, Tiến sĩ Daniel Mansfield và Norman Wildberger, một phó giáo sư tại Đại học New South Wales (UNSW) - Australia, đã xác định một chiếc máy tính bảng khác ở Babylon có chứa bảng lượng giác chính xác và lâu đời nhất thế giới. Vào thời điểm đó, họ suy đoán chiếc máy tính bảng này có thể đã được sử dụng trong thực tế, có thể là trong khảo sát hoặc xây dựng.
Máy tính bảng đó, có tên Plimpton 322, đã mô tả các tam giác vuông bằng cách sử dụng bộ ba số Pitago: Ba số nguyên trong đó tổng bình phương của hai số đầu tiên bằng bình phương của số thứ ba - ví dụ: 32 42 = 52.
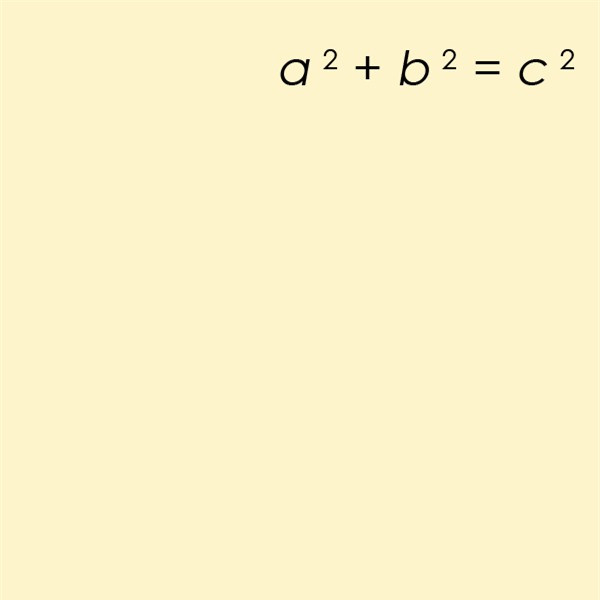
Hình ảnh động cho thấy ví dụ đơn giản nhất về bộ ba Pythagore. Nguồn: AmericanXplorer13 / Wikimedia / CC BY-SA 3.0
Sự xuất hiện của Plimpton 322 đặt Tiến sĩ Daniel Mansfield vào một nhiệm vụ tìm kiếm những máy tính bảng khác cùng thời kỳ có chứa bộ ba Pitago [hay Pythagore, bao gồm ba số nguyên dương a, b và c, sao cho a² b² = c²]. Cuối cùng, Si.427 xuất hiện!
"Si.427 giống như một mảnh đất được bán thu nhỏ. Trong văn tự chữ hình nêm, với các vết lõm hình nêm đặc trưng, Si.427 mô tả một cánh đồng có các khu vực đầm lầy, cũng như sàn đập và tháp gần đó.
Các hình chữ nhật mô tả cánh đồng có các cạnh đối diện với độ dài bằng nhau, cho thấy các nhà khảo sát thời đó đã nghĩ ra cách tạo ra các đường vuông góc chính xác hơn trước đây" - Tiến sĩ Daniel Mansfield nhận định.
"Giống như chúng ta ngày nay, khi một người cổ gắng tìm ra ranh giới đất đai của họ, họ sử dụng thiết bị GPS, còn thời xưa, họ dùng bộ ba Pitago".
Điều kinh ngạc
Và một sự thật khiến các nhà khoa học kinh ngạc đó là, mặc dù Plimpton 322 và Si.427 đều sử dụng bộ ba Pitago, nhưng CHÚNG LẠI XUẤT HIỆN TRƯỚC nhà toán học Hy Lạp Pythagoras hơn 1.000 năm.
[Pythagoras (phiên âm tiếng Pháp là Pytago) được xem là 'cha đẻ của số học'. Ông nổi tiếng với Định lý Pytago của tam giác vuông: a2 b2 = c2, với c là độ dài cạnh huyền, a và b là độ dài hai cạnh góc vuông].
Tiến sĩ Mansfield nói: "Một khi bạn hiểu bộ ba Pitago là gì, xã hội của bạn đã đạt đến một mức độ tinh vi toán học cụ thể. Si.427 chứa ba bộ ba Pitago: 3, 4, 5; 8, 15, 17; và 5, 12, 13".
Người Babylon đã sử dụng hệ đếm cơ số 60 - Hệ cơ số 60 của người Babylon là nền tảng để hôm nay chúng ta chia 1 phút thành 60 giây, 1 giờ thành 60 phút và 1 vòng tròn có 360 độ - khiến việc làm việc với các số nguyên tố lớn hơn 5 trở nên khó khăn.
Chiếc máy tính bảng Si.427, được mô tả trong một nghiên cứu trên tạp chí Foundations of Science, xuất hiện từ thời kỳ gia tăng sở hữu đất tư nhân.
Tiến sĩ Mansfield nói: "Bây giờ chúng ta biết người Babylon đang cần nó để giải quyết vấn đề gì. Bạn thấy đó, toán học đang được phát triển để giải quyết nhu cầu của thời đại."
Một điều khiến Tiến sĩ Mansfield khó hiểu về Si.427 là số thập phân giới tính "25:29" - tương tự như 25 phút 29 giây - được khắc bằng phông chữ lớn ở mặt sau của máy tính bảng.
"Đó có phải là một phần của phép tính mà họ đã thực hiện không? Đó có phải là một lĩnh vực mà tôi chưa từng biết không? Nó có phải là một phép đo của một cái gì đó không? Tôi thực sự khó chịu vì có quá nhiều thứ về máy tính bảng của người xưa. Bộ óc của họ thật vĩ đại!" - Tiến sĩ Mansfield kết luận.