Người đàn ông đó là Eratosthenes, một nhà toán học Hy Lạp và là người đứng đầu thư viện tại Alexandria.

Eratosthenes đã nghe nói rằng ở Syene, một thành phố phía nam Alexandria, không có bóng thẳng đứng nào được đổ vào buổi trưa ngày hạ chí, mặt trời chiếu thẳng trên đỉnh đầu. Ông tự hỏi liệu điều này có đúng ở Alexandria không.
Vì vậy, vào ngày 21 tháng 6, ông cắm một cây gậy thẳng xuống đất và chờ xem liệu có bóng đổ vào buổi trưa hay không. Hóa ra là có, và ông đo được cái bóng tạo ra một góc khoảng 7,2 độ.
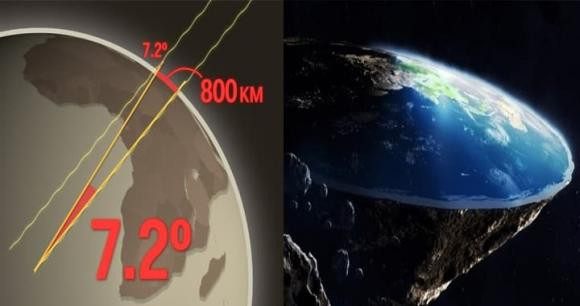
Nếu các tia sáng mặt trời chiếu vào cùng một góc vào cùng một thời điểm trong ngày và một cây gậy ở Alexandria đổ bóng trong khi một cây gậy ở Syene thì không, điều đó có nghĩa là bề mặt Trái đất bị cong. Và Eratosthenes có lẽ đã biết điều đó.
Ý tưởng về Trái đất hình cầu đã được Pythagoras đưa ra vào khoảng năm 500 trước Công nguyên và được Aristotle xác nhận vài thế kỷ sau đó. Nếu Trái đất thực sự là một hình cầu, thì Eratosthenes có thể sử dụng các quan sát của mình để ước tính chu vi của toàn bộ hành tinh.
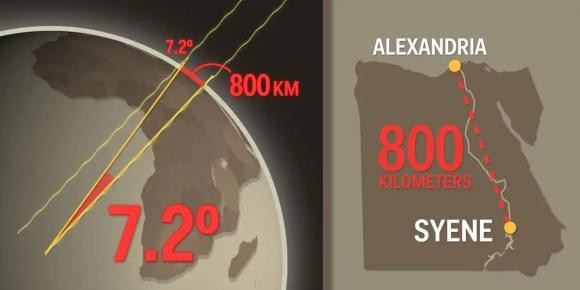
Vì sự khác biệt về độ dài 2 bóng gậy 7 độ ở Alexandria và Syene, điều đó có nghĩa là hai thành phố cách nhau 7 độ trên bề mặt 360 độ của Trái đất. Eratosthenes thuê một người đo khoảng cách giữa hai thành phố và được biết chúng cách nhau 5.000 stadia, tức là khoảng 800 km.
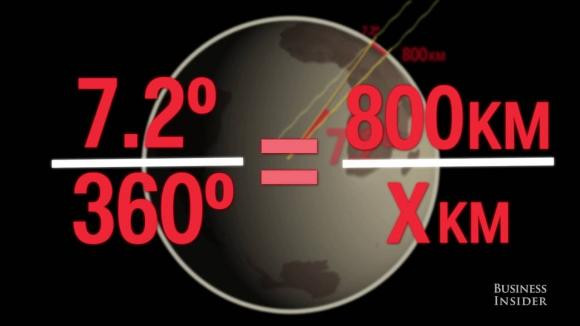
Sau đó, ông có thể sử dụng các tỷ lệ đơn giản để tìm chu vi Trái đất - 7,2 độ là 1/50 của 360 độ, vì vậy 800 nhân 50 bằng 40.000 km. Và cứ như thế, một người đàn ông 2200 năm trước đã tìm ra chu vi của toàn bộ hành tinh của chúng ta chỉ bằng một cây gậy và bộ não của mình.