


























Người Việt Nam chiếm 23,4% tỉ lệ trong số công dân mới nhập tịch.





Những gì còn lại sau vụ hoả hoạn thiêu rụi cửa hàng nội thất chỉ là cảnh ngổn ngang; 2 tiệm trà sữa và ĐTDĐ cũng bị cháy lan…
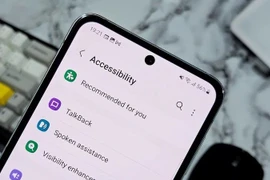
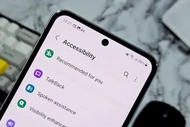
Các ngân hàng khuyến nghị người dùng Android tắt quyền Trợ năng cho ứng dụng lạ, tránh nguy cơ bị chiếm quyền và mất tiền trong tích tắc.

Bước sang giai đoạn hậu tam tai, có 3 con giáp được dự báo bước vào chu kỳ nảy lộc sinh tài mạnh mẽ.

Sừng sững giữa giao lộ Á – Âu của Istanbul, Hagia Sophia là công trình mang trong mình lớp lớp lịch sử tôn giáo và chính trị với chiều sâu gần 1.500 năm.

Ngôi nhà thiết kế tối giản, sử dụng gam màu trắng chủ đạo kết hợp cây xanh mang đến không gian sống yên tĩnh - xu hướng ngày càng phổ biến trong giới trẻ.

Accenture yêu cầu toàn bộ nhân viên phải chứng minh sử dụng AI, kể cả giám đốc. Ai không nâng cấp kỹ năng sẽ đối mặt nguy cơ mất việc.

Mặt trận Konstantinivka: "Cỗ máy xay thịt mới" của chiến trường Donbass; chiến thuật "bao vây - tiêu diệt" của Nga có thể đánh sập Kostiantynivka?

Diện thiết kế áo dài thả dáng trên đường phố San Francisco, cô nàng Youtuber Jenny Huỳnh khiến dân mạng 'lịm tim' bởi vẻ ngoài trong trẻo, ngọt ngào.

Mỗi độ Xuân về, Lùng Cúng (Nậm Có, Lào Cai) khoác sắc đào phai rực rỡ. Hoa nở khắp bản làng, vẽ nên mùa xuân bình yên giữa đại ngàn Tây Bắc.

Ngô Lan Hương khiến người hâm mộ không khỏi trầm trồ khi xuất hiện rực rỡ ngày đầu năm trong bộ cánh đỏ nổi bật, khoe trọn nhan sắc cuốn hút.

Từng được biết đến qua hội làng dịp Tết 2025, nữ đô vật Anh Thơ hiện vẫn là gương mặt được nhiều người quan tâm trên mạng xã hội.

Phanh Lee gây chú ý khi xuất hiện với vẻ đẹp nền nã, dịu dàng giữa không gian phố cổ, toát lên khí chất chuẩn quý cô Hà thành.

Trong không khí rộn ràng của những ngày đầu năm, 'rich kid' Joyce Phạm đã khiến cộng đồng mạng không khỏi trầm trồ khi tung ra bộ ảnh du xuân đầy ấn tượng.

Sau khi Tổng thống Mỹ ra lệnh công bố các hồ sơ mật liên quan UFO và sự sống ngoài hành tinh, nhiều người nhớ tới một lời tiên tri của bà Vanga.

Bản tiêu chuẩn của Lynk & Co 03 sẽ ra mắt Việt Nam vào tháng 9/2025, giá từ 800 triệu, dùng động cơ 1.5L tăng áp, cạnh tranh Honda Civic và Hyundai Elantra.

Hồ Rotomairewhenua hay còn gọi Hồ Xanh được xem là vùng nước trong xanh nhất thế giới với tầm nhìn khoảng 80m.

Sống trong những cánh rừng rậm rạp và đầm lầy ẩm ướt, chó bụi Nam Mỹ (Speothos venaticus) là một loài thú ăn thịt bí ẩn sở hữu nhiều đặc điểm đáng kinh ngạc.
Nhiều người nghĩ vuốt bỏ ứng dụng sẽ tiết kiệm pin, nhưng thực tế smartphone hiện đại thông minh hơn, thói quen này chỉ khiến máy hoạt động nặng nhọc hơn.

Theo tử vi 12 cung hoàng đạo ngày 25/2, Xử Nữ và Song Tử bứt phá khi nhận được sự ủng hộ. Đây là lúc cần tận dụng các mối quan hệ và phát huy sự tháo vát.

Iran sở hữu hệ thống phòng không đa lớp gồm S-300, Raad, Tor-M1 cùng radar cảnh giới hiện đại, tăng cường khả năng phòng thủ toàn diện.